Given:
The sum of the first three terms = 12
The sum of the first six terms = (−84).
To find:
The third term of a geometric progression.
Solution:
The sum of first n term of a geometric progression is:
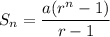
Where, a is the first term and r is the common ratio.
The sum of the first three terms is equal to 12, and the sum of the first six terms is equal to (−84).
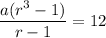 ...(i)
...(i)
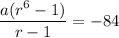 ...(ii)
...(ii)
Divide (ii) by (i), we get
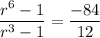
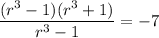
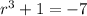
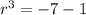
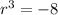
Taking cube root on both sides, we get
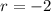
Putting
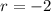 in (i), we get
in (i), we get
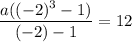
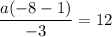
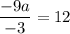
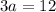
Divide both sides by 3.
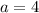
The nth term of a geometric progression is:
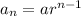
Where, a is the first term and r is the common ratio.
Putting
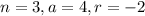 in the above formula, we get
in the above formula, we get
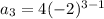
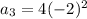
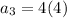
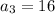
Therefore, the third term of the geometric progression is 16.