Question

The 11th term of an arithmetic progression is 14 and the sum of the first 26 terms is 416. Find the first term and the common difference.​

Answer 1

The first term is 6; the common difference in 0.8.

Explanation:

The nth term is:

`a_n = a_1 + (n - 1)d`

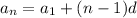
The sum of the first n terms is:

`S_n = (n(a_1 + a_n))/(2)`

`a_(n) = a_1 + (n - 1)d`

`a_(11) = a_1 + (11-1)d`

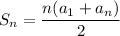
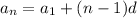
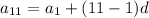
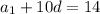`a_1 + 10d = 14` Equation 1

`S_n = (n(a_1 + a_n))/(2)`

`S_(26) = (26(a_1 + a_(26)))/(2)`

`(26(a_1 + a_1 + 25d)/(2) = 416`

`(52a_1 + 650d))/(2) = 416`

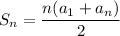
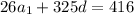`26a_1 + 325d = 416` Equation 2

Equation 1 and Equation 2 form a system of equations in 2 unknowns.

To eliminate a_1, subtract 26 times Eq. 1 from Eq. 2.

`65d = 52`

`d = (52)/(65)`

`d = (4)/(5) = 0.8`

`a_1 + 10d = 14`

`a_1 + 10 * 0.8 = 14`

`a_1 + 8 = 14`

`a_1 = 6`

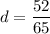
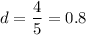
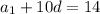
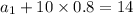
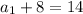
Answer:

The first term is 6; the common difference in 0.8.