Question

Two cars are facing each other. Car A is at rest while car B is moving toward car A with a constant velocity of 20 m/s. When car B is 100 from car A, car A begins to accelerate toward car B with a constant acceleration of 5 m/s/s. Let right be positive.

1) How much time elapses before the two cars meet? 2) How far does car A travel before the two cars meet? 3) What is the velocity of car B when the two cars meet?
4) What is the velocity of car A when the two cars meet?

Answer 1

Let's define t = 0s (the initial time) as the moment when Car A starts moving.

Let's find the movement equations of each car.

A:

We know that Car A accelerations with a constant acceleration of 5m/s^2

Then the acceleration equation is:

`A_a(t) = 5m/s^2`

To get the velocity, we integrate over time:

`V_a(t) = (5m/s^2)*t + V_0`

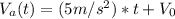
Where V₀ is the initial velocity of Car A, we know that it starts at rest, so V₀ = 0m/s, the velocity equation is then:

`V_a(t) = (5m/s^2)*t`

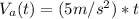
To get the position equation we integrate again over time:

`P_a(t) = 0.5*(5m/s^2)*t^2 + P_0`

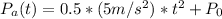
Where P₀ is the initial position of the Car A, we can define P₀ = 0m, then the position equation is:

`P_a(t) = 0.5*(5m/s^2)*t^2`

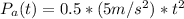
Now let's find the equations for car B.

We know that Car B does not accelerate, then it has a constant velocity given by:

`V_b(t) =20m/s`

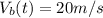
To get the position equation, we can integrate:

`P_b(t) = (20m/s)*t + P_0`

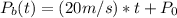
This time P₀ is the initial position of Car B, we know that it starts 100m ahead from car A, then P₀ = 100m, the position equation is:

`P_b(t) = (20m/s)*t + 100m`

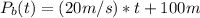
Now we can answer this:

1) The two cars will meet when their position equations are equal, so we must have:

`P_a(t) = P_b(t)`

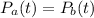
We can solve this for t.

`0.5*(5m/s^2)*t^2 = (20m/s)*t + 100m\\(2.5 m/s^2)*t^2 - (20m/s)*t - 100m = 0`

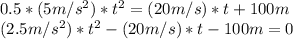
This is a quadratic equation, the solutions are given by the Bhaskara's formula:

`t = (-(-20m/s) \pm √((-20m/s)^2 - 4*(2.5m/s^2)*(-100m)) )/(2*2.5m/s^2) = (20m/s \pm 37.42 m/s)/(5m/s^2)`

We only care for the positive solution, which is:

`t = (20m/s + 37.42 m/s)/(5m/s^2) = 11.48 s`

Car A reaches Car B after 11.48 seconds.

2) How far does car A travel before the two cars meet?

Here we only need to evaluate the position equation for Car A in t = 11.48s:

`P_a(11.48s) = 0.5*(5m/s^2)*(11.48s)^2 = 329.48 m`

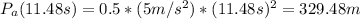
3) What is the velocity of car B when the two cars meet?

Car B is not accelerating, so its velocity does not change, then the velocity of Car B when the two cars meet is 20m/s

4) What is the velocity of car A when the two cars meet?

Here we need to evaluate the velocity equation for Car A at t = 11.48s

`V_a(t) = (5m/s^2)*11.48s = 57.4 m/s`