Answer:
The probability of a bulb lasting for between 480 and 526 hours=0.74454
Explanation:
We are given that
Standard deviation of the lifetime,
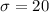 hours
hours
Mean,
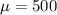 hours
hours
We have to find the probability of a bulb lasting for between 480 and 526 hours.
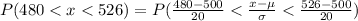
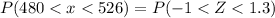
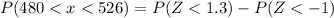
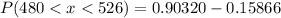
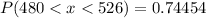
Hence, the probability of a bulb lasting for between 480 and 526 hours=0.74454