Hi there!
We can begin by solving the left side:
tan²Θ - sin²Θ =
Rewrite tan:
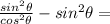
Multiply sin²Θ by cos²Θ to get a common denominator:
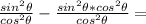
Subtract:
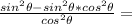
Factor out sin²Ф from the numerator:
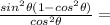
Rewrite 1 - cos²Ф as sin²Ф (Pythagorean identity)
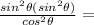
Simplify:
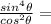
Split into sin and tan:
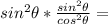
Rewrite:
