Answer:
Yes, P(E1)=P(E2)
Explanation:
We are given that
Number of dice=3
Total outcomes of 1 die=6
Therefore,
Total number of outcomes =
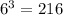
E1={{(1,4,6),(2,3,6),(1,5,5),(2,4,5),(3,3,5),(3,4,4)}
E2={(1,5,6),(2,4,6),(3,3,6),(2,5,5),(4,4,4),(3,4,5)}
We have to show that E1 and E2 have the same probability P(E1) = P(E2).
Probability,
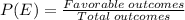
Using the formula

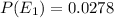
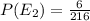
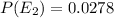
Hence, P(E1)=P(E2)