Question

A few people gather together to play a game in which one needs to roll 3 six-sided dice. One person notices that the sum of the number of spots on three dice comes up as 11 (the event E1) more often than it does 12 (the event E2) even though it looks like it should be even. This person argues as follows: E1 occurs in just six ways:

{(1,4,6),(2,3,6),(1,5,5),(2,4,5),(3,3,5),(3,4,4)}, and E2 occurs also in just six ways: {(1,5,6),(2,4,6),(3,3,6),(2,5,5),(4,4,4),(3,4,5)}.

Therefore E1 and E2 have the same probability P(E1) = P(E2). Why isn’t it?

Answer 1

Yes, P(E1)=P(E2)

Explanation:

We are given that

Number of dice=3

Total outcomes of 1 die=6

Therefore,

Total number of outcomes =
`6^3=216`

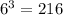
E1={{(1,4,6),(2,3,6),(1,5,5),(2,4,5),(3,3,5),(3,4,4)}

E2={(1,5,6),(2,4,6),(3,3,6),(2,5,5),(4,4,4),(3,4,5)}

We have to show that E1 and E2 have the same probability P(E1) = P(E2).

Probability,
`P(E)=(Favorable\;outcomes)/(Total\;outcomes)`

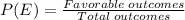
Using the formula

`P(E_1)=(6)/(216)`

`P(E_1)=0.0278`

`P(E_2)=(6)/(216)`

`P(E_2)=0.0278`

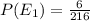
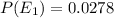
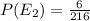
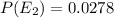
Hence, P(E1)=P(E2)