Question

Which function matches this graph?

f(x)=x2−3f ( x ) = x 2 − 3
f(x)=x2+9f x = x 2 + 9

f(x)=x2−6x+9f ( x ) = x 2 − 6 x + 9
f(x)=x2+6x+9f ( x ) = x 2 + 6 x + 9

Answer 1

`\large\boxed{\sf f(x) = x^2-6x+9}`

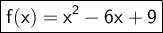
Explanation:

We are here given a graph of a equation and we are interested in finding the equation .

From the given graph we can see that it cuts the x axis at point (3,0) . This graph represents a quadratic function and its two zeroes are 3,3 . We can write the equation using the two zeroes .

Say if the zeroes of the quadratic equation are p and q , then the quadratic equation can be written as ,

`\longrightarrow (x-p)(x-q)=0`

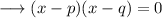
And the quadratic function can be written as ,

`\longrightarrow f(x)= k[ (x-p)(x-q)]`

where k is a constant .In this case k = 1 . So we can write the function as ,

`\longrightarrow f(x) = (x-3)(x-3)`

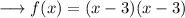
Distribute ,

`\longrightarrow f(x)= x (x-3)-3(x-3)`

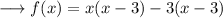
Simplify by opening the brackets,

`\longrightarrow f(x) = x^2-3x -3x +9`

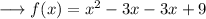
Add like terms,

`\longrightarrow \underline{\underline{f(x) = x^2-6x+9}}`

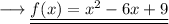
And we are done!