Question

A person jumps out of an airplane above the surface of the Earth, and falls a distance h before opening their parachute. Once the prachute is open the person coasts to the ground a distance d at constant velocity.

a. The work done on the person by the Earth is:
b. The change in gravitational potential energy of the person + Earch system is:

Answer 1

a) W_total = mg (2h + d) , b) E_total = - mg (h + d)

Step-by-step explanation:

a) We must solve this problem in two parts, the first for the accelerated movement and the second for the movement with constant speed

Let's look for work for the part that is in free fall

y = y₀ + v₀ t - ½ g t²

when he jumps out of a plane his vertical speed is zero

y =y₀ - ½ g t²

dy = 0 - ½ g 2t dt

the work in this first part is

W₁ = ∫ F dy

W₁ = mg ∫ g t dt

W₁ = m g² t² / 2

the time it takes to travel the distance y₀-y = h is

y₀-y = ½ g t²

t =
`√(2h/g)`

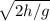
we substitute

W₁ = m g² 2h / g

W₁ = m g 2h

now we look for the work for the part with constant speed

since the velocity is constant let's use the uniform motion ratio

W₂ = F d

W₂ = mg d

the total work is

W_total = W₁ + W₂

W_total = 2mgh + m gd

W_total = mg (2h + d)

b) The change in gravitational potential energy

U = mg Δy

in the part with accelerated movement

U₁ = mg h

in the part with uniform movement

U₂ = mg d

the total potential energy is

E_total = U₁ + U₂

E_total = - mg (h + d)