Answer:
By these examples you are able to see that the square of an odd number is always 1 more than a multiple of 4.
Explanation:
For examples,
Let's consider squares of 3, 11, 25, 37 and 131.

8 is a multiple of 4, and 9 is more than 8.
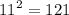
120 is a multiple of 4 and 121 is one more than it.
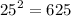
624 is a multiple of 4 and 625 is one more than it.
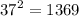
1368 is a multiple of 4 and 1369 is one more than 1368.
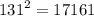
17160 is a multiple of 4.