Answer:
Speed of the river =
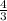 km per hour
km per hour
Explanation:
Speed of the boat in still water = 4 km per hour
Let the speed of the river = v km per hour
Speed of the boat upstream = (4 - v) km per hour
Time taken to cover 6 km =
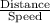
=
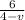 hours
hours
Speed of the boat downstream = (4 + v) km per hour
Time taken to cover 12 km =
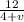 hours
hours
Since, time taken by the boat in both the cases is same,
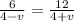
6(4 + v) = 12(4 - v)
24 + 6v = 48 - 12v
12v + 6v = 48 - 24
18v = 24
v =
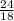
v =
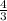 km per hour
km per hour