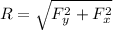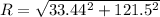Answer:
a)

b)
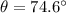
Step-by-step explanation:
From the question we are told that:
1st segment
243km at Angle=30
2nd segment
178km West
Resolving to the X axis
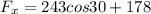
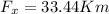
Resolving to the Y axis
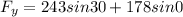
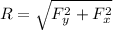
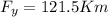
Therefore
Generally the equation for Directional Angle is mathematically given by
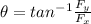
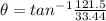
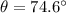
Generally the equation for Magnitude is mathematically given by