Answer:
hey there hope this answer helps you out
Explanation:
we have two functions f(x) and g(x) such that
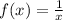
and
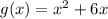
solving for f ° g, we'll substitute the x in f(x) by the value of g(x)
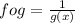
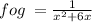
taking x common in denominator
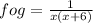
for a function to exist it should not have 0 in its denominator
checking the values of x for which the denominator of f ° g becomes 0 :-
so the function doesn't exist at values x = 0, -6
So, 0, -6 cannot be in the domain of f°g