Answer:
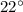
Explanation:
Line
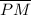 is a diameter of the circle because it passes through the circle's center O. Therefore, arc
is a diameter of the circle because it passes through the circle's center O. Therefore, arc
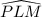 must be 180 degrees, as these are 360 degree in a circle.
must be 180 degrees, as these are 360 degree in a circle.
We can then find the measure of arc
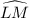 :
:

Arc
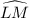 is formed by angle
is formed by angle
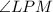 . Define an inscribed angle by an angle with a point on the circle creating an arc on the circumference of the circle. The measure of an inscribed angle is exactly half of the measure of the arc it forms.
. Define an inscribed angle by an angle with a point on the circle creating an arc on the circumference of the circle. The measure of an inscribed angle is exactly half of the measure of the arc it forms.
Therefore, the measure of
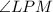 must be:
must be:
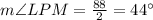
Similarly, the measure of
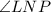 must be:
must be:
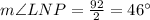
Angles
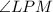 and
and
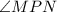 form angle
form angle
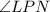 , which is one of the three angles in
, which is one of the three angles in
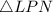 . Since the sum of the interior angles of a triangle add up to 180 degrees, we have:
. Since the sum of the interior angles of a triangle add up to 180 degrees, we have:
