Answer:
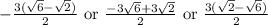
Explanation:
There are multiple ways to achieve and even express the exact answer to this problem. Because the exact value of
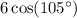 is a non-terminating (never-ending) decimal, it does not have a finite number of digits. Therefore, you cannot express it as an exact value as a decimal, as you'd either have to round or truncate.
is a non-terminating (never-ending) decimal, it does not have a finite number of digits. Therefore, you cannot express it as an exact value as a decimal, as you'd either have to round or truncate.
Solution 1 (Cosine Addition Identity):
Nonetheless, to find the exact value we must use trigonometry identities.
Identity used:
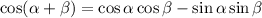
Notice that
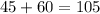 and therefore we can easily solve this problem if we know values of
and therefore we can easily solve this problem if we know values of
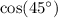 ,
,
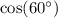 ,
,
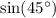 , and
, and
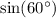 , which is plausible as they are all key angles on the unit circle.
, which is plausible as they are all key angles on the unit circle.
Recall from either memory or the unit circle that:
Therefore, we have:
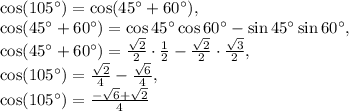
Since we want the value of
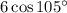 , simply multiply this by 6 to get your final answer:
, simply multiply this by 6 to get your final answer:
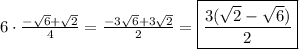
Solution 2 (Combination of trig. identities):
Although less plausible, you may have the following memorized:

If so, we can use the following trig. identity:
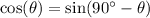 (the cosine of angle theta is equal to the sine of the supplement of angle theta - the converse is also true)
(the cosine of angle theta is equal to the sine of the supplement of angle theta - the converse is also true)
Therefore,
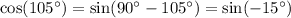
Recall another trig. identity:
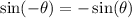 and therefore:
and therefore:
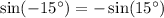
Multiply by 6 to get:
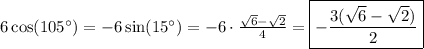 (alternative final answer).
(alternative final answer).