Question

If the point ((4,-2) what is included in a direct viration relationship which point also belongs and variation

Answer 1

The answer is "This direct variant (-4,2) is part of it".

Explanation:

The equation expresses its direct variation relation

`y = mx ........ (1)`

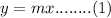
Where x and y vary directly, and k vary continuously.

Now so the point (4,-2) is in the direct relation of variation, so from equation (1) we are given,
`-2 = 4m`

`\to m=-(1)/(2)`

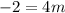
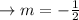
The equation (1) is therefore converted into

`\to y=-(1)/(2)x \\\\\to x + 2y = 0 ......... (2)`

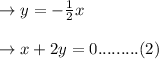
Then only the point (-4,2) satisfies the connection with the four possibilities (2). Therefore (-4,2) is a direct variant of this.