Question

A student ran out of time on a multiple choice exam and randomly guessed the answers for two problems. Each problem had 5 answer choices - a, b, c, d, e- and only one correct answer. What is the probability that she answered neither of the problems correctly? Do not round your answer. (If necessary, consult a list of formulas.)​

Answer 1

there is a 64% chance that the student got both problems wrong

a 32% chance that they got only 1 correct

and a 4% chance that they got both correct

Explanation:

There are 25 total possible combinations of answers, with 8 possible combinations where the student would get 1 answer right, and 1 combination where the student would get both answers correct.

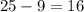
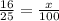
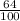
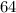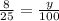
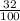
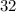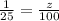
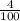
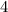`25-9=16`

`(16)/(25) =(x)/(100)`

`(64)/(100)`

`64`%

`(8)/(25) =(y)/(100)`

`(32)/(100)`

`32`%

`(1)/(25) =(z)/(100)`

`(4)/(100)`

`4`%