Answer:
The remainder is 3x - 4
Explanation:
[Remember]
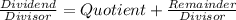
So,
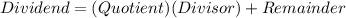
In this case our dividend is always P(x).
Part 1
When the divisor is
 , the remainder is
, the remainder is
 , so we can say
, so we can say
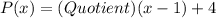
In order to get rid of "Quotient" from our equation, we must multiply it by 0, so

When solving for
 , we get
, we get
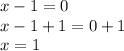
When
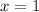 ,
,
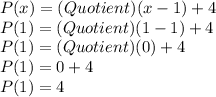
--------------------------------------------------------------------------------------------------------------
Part 2
When the divisor is
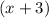 , the remainder is
, the remainder is
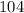 , so we can say
, so we can say

In order to get rid of "Quotient" from our equation, we must multiply it by 0, so
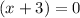
When solving for
 , we get
, we get
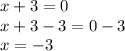
When
 ,
,
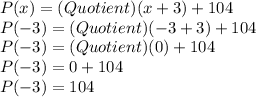
--------------------------------------------------------------------------------------------------------------
Part 3
When the divisor is
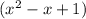 , the quotient is
, the quotient is
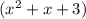 , and the remainder is
, and the remainder is
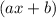 , so we can say
, so we can say
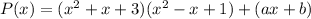
From Part 1, we know that
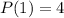 , so we can substitute
, so we can substitute
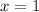 and
and
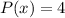 into
into
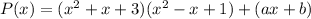
When we do, we get:
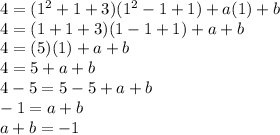
We will call
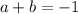 equation 1
equation 1
From Part 2, we know that
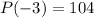 , so we can substitute
, so we can substitute
 and
and
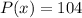 into
into
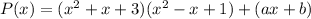
When we do, we get:
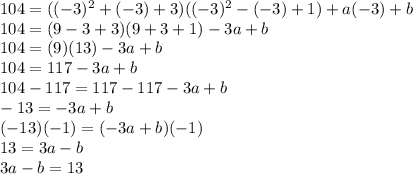
We will call
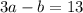 equation 2
equation 2
Now we can create a system of equations using equation 1 and equation 2
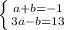
By adding both equations' right-hand sides together and both equations' left-hand sides together, we can eliminate
 and solve for
and solve for

So equation 1 + equation 2:

Now we can substitute
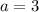 into either one of the equations, however, since equation 1 has less operations to deal with, we will use equation 1.
into either one of the equations, however, since equation 1 has less operations to deal with, we will use equation 1.
So substituting
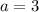 into equation 1:
into equation 1:
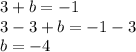
Now that we have both of the values for
 and
and
 , we can substitute them into the expression for the remainder.
, we can substitute them into the expression for the remainder.
So substituting
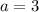 and
and
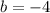 into
into
 :
:
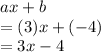
Therefore, the remainder is
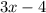 .
.