Answer with Step-by-step explanation:
We are given that
Side of cube, x=30 cm
Error in measurement of edge,
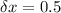 cm
cm
(a)
Volume of cube,
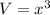
Using differential
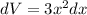
Substitute the values
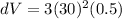
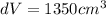
Hence, the maximum possible error in computing the volume of the cube
=
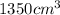
Volume of cube,
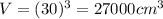
Relative error=
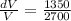
Relative error=0.05
Percentage error=
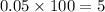 %
%
Hence, relative error in computing the volume of the cube=0.05 and
percentage error in computing the volume of the cube=5%
(b)
Surface area of cube,
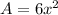
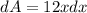
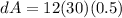
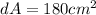
The maximum possible error in computing the volume of the cube=
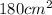
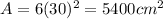
Relative error=
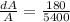
Relative error in computing the volume of the cube=0.033
The percentage error in computing the volume of the cube=
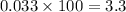 %
%