Answer:
The average value of the cost function over the interval is of $23,500.
Explanation:
Average value of a function:
The average value of a function, over an inteval [a,b], is given by:
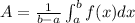
In this case:
Function
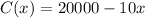 , interval with
, interval with
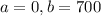
So
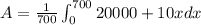
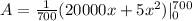
So
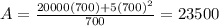
The average value of the cost function over the interval is of $23,500.