Question

Y = RootIndex 3 StartRoot x EndRoot. y = negative (0.4) RootIndex 3 StartRoot x minus 2 EndRoot

Which of the following describes the graph of the transformed function compared with the parent function? Select all that apply.

Answer 1

Answers:

-reflected over the x-axis

-translated 2 units right

-compressed by a factor of 0.4

Answer 2

- Reflected over the x-axis

- Compressed by a factor of 0.4.

- Translated 2 units left

Explanation:

Given

`y = \sqrt[3]{x}`

`y' = -(0.4)\sqrt[3]{x-2}`

Required

The transformation from y to y'

First, y is reflected over the x-axis.

The transformation rule is:

`(x,y) \to (x,-y)`

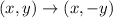
So, we have:

`y = \sqrt[3]{x}` becomes

`y' = -\sqrt[3]{x}`

Next, it was compressed by a scale factor of 0.4

The rule is:

`y' = k * y`

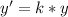
Where k is the scale factor (i.e. k = 0.4)

So, we have:

`y' = 0.4 * -\sqrt[3]{x}`

`y' = -(0.4)\sqrt[3]{x}`

Lastly, the function is translated 2 units left;

The rule is:

`(x,y) \to (x-2,y)`

So, we have:

`y' = -(0.4)\sqrt[3]{x - 2}`