Question

Can someone please help me solve this? thank you!:)

Answer 1

First, we need to set up our two equations. For the picture of this scenario, there is one length (L) and two widths (W) because the beach removes one of the lengths. We will have a perimeter equation and an area equation.

P = L + 2W

A = L * W

Now that we have our equations, we need to plug in what we know, which is the 40m of rope.

40 = L + 2W

A = L * W

Then, we need to solve for one of the variables in the perimeter equation. I will solve for L.

L = 40 - 2W

Now, we can substitute the value for L into L in the area equation and get a quadratic equation.

A = W(40 - 2W)

A = -2W^2 - 40W

The maximum area will occur where the derivative equals 0, or at the absolute value of the x-value of the vertex of the parabola.

V = -b/2a

V = 40/2(2) = 40/4 = 10

Derivative:

-4w - 40 = 0

-4w = 40

w = |-10| = 10

To find the other dimension, use the perimeter equation.

40 = L + 2(10)

40 = L + 20

L = 20m

Therefore, the dimensions of the area are 10m by 20m.

Hope this helps!

Answer 2

Width: 10 m

Length: 20 m

Explanation:

Hi there!

Let w be equal to the width of the enclosure.

Let l be equal to the length of the enclosure.

1) Construct equations

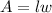`A=lw` ⇒ A represents the area of the enclosure.

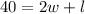`40=2w+l` ⇒ This represents the perimeter of the enclosure. Normally, P=2w+2l, but because one side isn't going to use any rope (sandy beach), we remove one side from this equation.

2) Isolate one of the variables in the second equation

`40=2w+l`

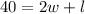
Let's isolate l. Subtract 2w from both sides.

`40-2w=2w+l-2w\\40-2w=l`

3) Plug the second equation into the first

`A=lw\\A=(40-2w)w\\A=40w-2w^2\\A=-2w^2+40w`

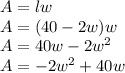
Great! Now that we have a quadratic equation, we can do the following:

1. Solve for its zeros/w-intercepts.
2. Take the average of the zeros to find the w-variable of the vertex. (The area (A) in relation to the width of the swimming area (w) is what we've established in this equation, and the area (A) is greatest at the vertex. Finding the value of w of the vertex will tell us what the width needs to be for the area to be at a maximum.)
3. Plug this w value into one of the equations to solve for l

4) Solve for w

`A=-2w^2+40w`

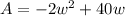
Factor out -2w

`A=-2w(w-20)`

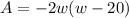
For A to equal 0, w=0 or w=20.

The average of 0 and 20 is 10, so the width that will max the area is 10 m.

5) Solve for l

`40=2w+l`

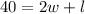
Plug in 10 as w

`40=2(10)+l\\40=20+l\\l=20`

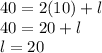
Therefore, the length of 20 m will max the area.

I hope this helps!