Answer:
y=
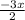
Explanation:
Hi there!
We need to find the equation of the line that passes through the origin (the point (0,0)) and (-2,3)
There are 3 ways to write the equation of the line, although the most common way is slope-intercept form.
Slope-intercept form is given as y=mx+b, where m is the slope and b is the y intercept
So we need to find the slope of the line first
The formula for the slope (m) calculated from two points
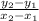 where (
where (
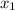 ,
,
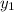 ) and (
) and (
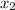 ,
,
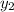 ) are points
) are points
We have the needed information to calculate the slope, but let's label the values of the points to avoid any confusion
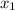 =0
=0
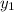 =0
=0
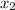 =-2
=-2
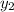 =3
=3
Now substitute their values into the equation and find m
m=
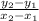
m=
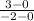
subtract
m=
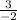
so the slope of the line is
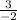 . It can also be rewritten as
. It can also be rewritten as
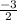
Here is the equation of the line so far:
y=
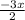 +b
+b
we need to find b
As the equation passes through both (0,0) and (-2,3), we can use either one of them to solve for b
Let's take (0,0) for this case
Substitute 0 as x and 0 as y
0=-
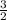 (0)+b
(0)+b
multiply
0=0+b
add 0 to both sides
0=b
So b is 0
The equation of the line therefore is y=
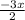
Hope this helps!