Answer:
2.5 years
Explanation:
The given amount invested, which is the principal, P = $16,800
The simple interest rate, R = 5% per annum
The intended total value of the investment, A = $18,900
The simple interest on the principal, I = A - P
∴ I = $18,900 - $16,800 = $2,100
The formula for the simple interest, I, is given as follows;

Therefore, we have;

Plugging in the values, gives;
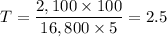
The time it will take the investment to grow to $18,900 is T = 2.5 years