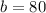Answer:
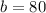 °
°
Explanation:
The central angles theorem states that the measure of an angle whose vertex is the center of the circle is equivalent to the arc surrounding it. One can apply this here by stating that the measure of the arc surrounding the (90) degree angle is (90) degrees.
The total degree measure of a circle is (360). Thus one can form an equation and solve it to find the measure of the arc surrounding the angle (b). Call the arc surrounding angle (b); (
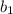 ).
).
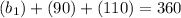
Simplify,
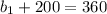
Inverse operations,
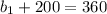

The peripheral angles theorem states that if the vertex of an angle formed between a tangent and a chord, is on the circumference (outer edge) of a circle, then the measure of the angle is equal to half of the measure of the surrouding arc. Please note that a chord is a line segment in a circle that intersects the circle in two points. A tangent is a line segment that intersects a circle at one point. One can apply this here by stating the following,
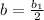
Substitute,
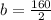
Solve,