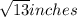remember the pythagorean theorem:
a² + b² = c²
where c is the hypotenuse.
so:
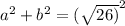
the square and the square root cancel each other out, so...
a² + b² = 26
we know that a and b are of equal length given the angles.
so it's
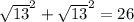
here the squares and square roots also cancel, but to keep the equation from the formula true we need to write them. that makes the difference between optional and B
Option A is correct,