Answer:
Area of square = 100 square cm
Explanation:
Let the sides of a square be = a
Perimeter of a square = 4a
Let area of square =
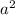
Let the Length of rectangle be =
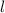
Given: width of the rectangle = 6 cm
Area of rectangle = length x breadth
Perimeter of rectangle and square is equal.
That is,
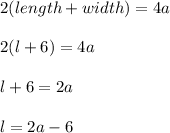
Therefore ,
Area of rectangle
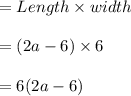
Given area of rectangle is 16 less than area of square.
That is ,
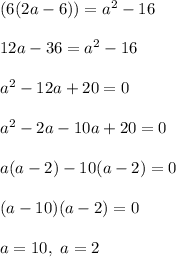
Check which value of 'a ' satisfies the equation:
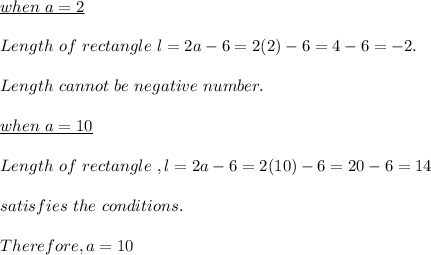
That is , side of the sqaure = 10
Therefore , area of the square = 10 x 10 = 100 square cm.