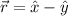Question

Which equation describes the summer for two vectors plotted below?

Answer 1

B

Explanation:

Answer 2

An equation that best describes the sum of the two vectors plotted above include the following: A.
`\vec r =\hat{x} - \hat{y}`

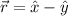
In Mathematics and Science, the head to tail method of adding two (2) vectors involve drawing the first vector (
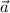`\vec a`) on a cartesian coordinate and then placing the tail of the second vector (
`\vec b`) at the head of the first vector. Lastly, the resultant vector is then drawn from the tail of the first vector (
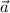`\vec a`) to the head of the second vector (
`\vec b`).

By critically observing the graph shown above, we can logically deduce that the head of the vector intersects the point (1, -1). Therefore, the resultant of the two (2) vectors is a vector with an x-intercept at 1 and a y-intercept at -1.

In this context, an equation that best describes the sum of the two vectors plotted above can be written as follows:

`\vec r =\hat{x} - \hat{y}`