Answer:
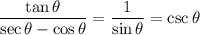
Explanation:
We have the expression:
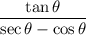
And we want to write the expression in terms of sine and cosine and simplify.
Thus, let tanθ = sinθ / cosθ and secθ = 1 / cosθ. Substitute:
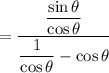
Multiply both layers by cosθ:
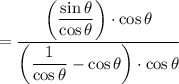
Distribute:
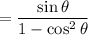
Recall from the Pythagorean Theorem that sin²θ + cos²θ = 1. Hence, 1 - cos²θ = sin²θ. Substitute and simplify:
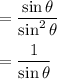
We can convert this to cosecant if we wish.