Question

An equation, f, has a domain of all whole numbers and has a range of all real numbers. A) Does the equation

represent a function? B) Explain why or why not. C) provide examples in either case, (and include your reasoning why
you chose this equation for your example.)

Answer 1

f is not a function

Explanation:

Given

Domain: Whole numbers

Range: Real numbers

Required

Is f a function

Base on the given parameters, f is not a function because:

There are more real numbers than whole numbers

And this implies that at least one element in the domain will have more than one corresponding elements in the range. i.e. one-to-many or many-to-many relationship

For a relation to be regarded as a function, the relationship has to be one-to-one or many-to-one

i.e. 1 or many domain elements to 1 element in the range.

An example is:

`\begin{array}{ccccc}x & {1} & {9} & {9} & {0} \ \\ f(x) & {1.5} & {3.2} & {-3.5} & {0.1} \ \end{array}`

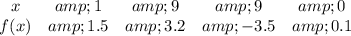
In the above function

The domain (i.e. x values) are whole numbers

The range (i.e. y values) are real numbers

However,

9 points to 3.2 and -3.5

So, the relation is not a function.