Question

Replace ∗ with a monomial so that the trinomial may be represented by a square of a binomial: b2 + 20b +*

Answer 1

Given:

The expression is:

`b^2+20b`

To find:

The a monomial so that the trinomial may be represented by a square of a binomial.

Solution:

If an expression is
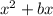`x^2+bx`, then be need to add square of half of coefficient of x, i.e.,
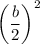`\left((b)/(2)\right)^2` in the given expression to make in perfect square.

We have,

`b^2+20b`

Here, coefficient of b is 20,so wee need to add square of half of coefficient of b, i.e.,
`\left((20)/(2)\right)^2`.

`\left((20)/(2)\right)^2=10^2`

`\left((20)/(2)\right)^2=100`

Therefore, we need to add 100 to make
`b^2+20b` a perfect square binomial.