Answer:
About 0.2076 or 20.76%.
Explanation:
Recall that compound interest is given by the formula:
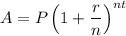
Where A is the final amount, P is the principal, r is the interest rate, n is the number of times the interest is applied per year, and t is the number of years.
Since Hannah wants to turn an $8,000 investment into $33,000 in seven years compounded quarterly, we want to solve for r given that P = 8000, A = 33000, n = 4, and t = 7. Substitute:
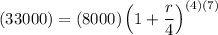
Simplify and divide both sides by 8000:
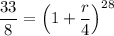
Raise both sides to the 1/28th power:
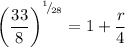
Solve for r. Hence:
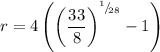
Use a calculator. Hence:
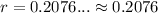
So, the quarterly rate of interest must be 0.2076, or about 20.76%.