Question

Calculate the percent dissociation of benzoic acid C6H5CO2H in a 1.3M aqueous solution of the stuff. You may find some useful data in the ALEKS Data resource. Round your answer to 2 significant digits.

Answer 1

the percent dissociation is 0.69 %

Step-by-step explanation:

Given the data in the question;

benzoic acid C₆H₅CO₂H

C₆H₅COOH
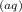`_{(aq)` ⇔ C₆H₅COO
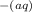`_{-(aq)` + H
`_{+(aq)`

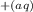
Ka = [C₆H₅COO- ][ H+ ] / [ C₆H₅COOH ] = 6.28 × 10⁻⁵

given that it dissociated in a 1.3 M aqueous solution.

so Initial concentration is;

[ C₆H₅COOH ] = 1.3

[C₆H₅COO- ] = 0

[ H+ ] = 0

Change in concentration

[ C₆H₅COOH ] = -x

[C₆H₅COO- ] = +x

[ H+ ] = +x

Concentration equilibrium

[ C₆H₅COOH ] = 1.3 - x

[C₆H₅COO- ] = +x

[ H+ ] = +x

Hence,

x² / ( 1.3 - x ) = 6.28 × 10⁻⁵

6.28 × 10⁻⁵( 1.3 - x ) = x²

8.164 × 10⁻⁵ - 6.28 × 10⁻⁵x = x²

x² + 6.28 × 10⁻⁵x - 8.164 × 10⁻⁵ = 0

solve for x

ax² + bx - c = 0

x = [ -b ± √( b² - 4ac ) ] / [ 2a ]

we substitute

x = [ -6.28 × 10⁻⁵ ± √( (6.28 × 10⁻⁵)² - (4 × 1 × -8.164 × 10⁻⁵ ) ) ] / [ 2 × 1 ]

x = [ -6.28 × 10⁻⁵ ± 0.01807 ] / [ 2]

x = [ -6.28 × 10⁻⁵ - 0.01807 ] / [ 2] or [ -6.28 × 10⁻⁵ + 0.01807 ] / [ 2]

x = -0.0090664 or 0.0090036

so x = 0.0090036

hence

[ H+ ] = +x = 0.0090036 M

[C₆H₅COO- ] = +x = 0.0090036 M

Initial concentration of [ C₆H₅COOH ] = 1.3 M

concentration of C₆H₅COOH dissociated = 0.0090036 M

percent dissociation of C₆H₅COOH will be;

⇒ ( 0.0090036 M / 1.3 M ) × 100 = 0.69 %

Therefore, the percent dissociation is 0.69 %