Answer:
the frequency of this mode of vibration is 138.87 Hz
Step-by-step explanation:
Given;
length of the copper wire, L = 1 m
mass per unit length of the copper wire, μ = 0.0014 kg/m
tension on the wire, T = 27 N
number of segments, n = 2
The frequency of this mode of vibration is calculated as;
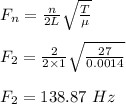
Therefore, the frequency of this mode of vibration is 138.87 Hz