Question

A mass is attached to the end of a spring and set into oscillation on a horizontal frictionless surface by releasing it from a compressed position. The record of time is started when the oscillating mass first passes through the equilibrium position, and the position of the mass at any time is described by

Answer 1

The question is incomplete. The complete question is :

A mass is attached to the end of a spring and set into oscillation on a horizontal frictionless surface by releasing it from a compressed position. The record of time is started when the oscillating mass first passes through the equilibrium position, and the position of the mass at any time is described by x = (4.7 cm)sin[(7.9 rad/s)πt].

Determine the following:

(a) frequency of the motion

(b) period of the motion

(c) amplitude of the motion

(d) first time after t = 0 that the object reaches the position x = 2.6 cm

Solution :

Given equation : x = (4.7 cm)sin[(7.9 rad/s)πt].

Comparing it with the general equation of simple harmonic motion,

x = A sin (ωt + Φ)

A = 4.7 cm

ω = 7.9 π

a). Therefore, frequency,
`$f=(\omega)/(2 \pi)$`

`$=(7.9 \pi)/(2 \pi)$`

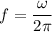
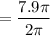
= 3.95 Hz

b). The period,
`$T=(1)/(f)$`

`$T=(1)/(3.95)`

= 0.253 seconds

c). Amplitude is A = 4.7 cm

d). We have,

x = A sin (ωt + Φ)

`$x_t=4.7 \sin (7.9 \pi t)$`

`$2.6 = 4.7 \sin (7.9 \pi t)$`

`$\sin (7.9 \pi t) = (26)/(47)$`

`$7.9 \pi t = \sin^(-1)\left((26)/(47)\right)$`

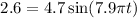
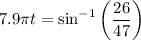
Hence, t = 0.0236 seconds.