The question is incomplete. The complete question is :
The breaking strengths of cables produced by a certain manufacturer have a mean of 1900 pounds, and a standard deviation of 65 pounds. It is claimed that an improvement in the manufacturing process has increased the mean breaking strength. To evaluate this claim, 150 newly manufactured cables are randomly chosen and tested, and their mean breaking strength is found to be 1902 pounds. Assume that the population is normally distributed. Can we support, at the 0.01 level of significance, the claim that the mean breaking strength has increased?
Solution :
Given data :
Mean, μ = 1900
Standard deviation, σ = 65
Sample size, n = 150
Sample mean,
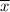 = 1902
= 1902
Level of significance = 0.01
The hypothesis are :
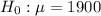
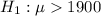
Test statics :
We use the z test as the sample size is large and we know the population standard deviation.
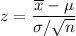
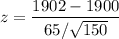
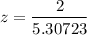
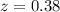
Finding the p-value:
P-value = P(Z > z)
= P(Z > 0.38)
= 1 - P(Z < 0.38)
From the z table. we get
P(Z < 0.38) = 0.6480
Therefore,
P-value = 1 - P(Z < 0.38)
= 1 - 0.6480
= 0.3520
Decision :
If the p value is less than 0.01, then we reject the
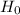 , otherwise we fail to reject
, otherwise we fail to reject
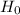 .
.
Since the value of p = 0.3520 > 0.01, the level of significance, then we fail to reject
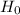 .
.
Conclusion :
At a significance level of 0.01, we have no sufficient evidence to support that the mean breaking strength has increased.