Answer:
0.1512 = 15.12% probability that fewer than four tornadoes occur in a three-week period.
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
In a given region, the number of tornadoes in a one-week period is modeled by a Poisson distribution with mean 2
Three weeks, so

Calculate the probability that fewer than four tornadoes occur in a three-week period.
This is:
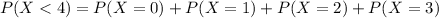
In which

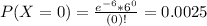
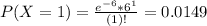
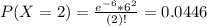
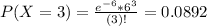
Then
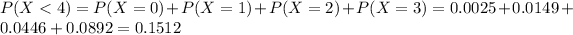
0.1512 = 15.12% probability that fewer than four tornadoes occur in a three-week period.