Question

4. One in four people in the US owns individual stocks. You randomly select 12 people and ask them if they own individual stocks. a. Find the mean, variance, and standard deviation of the resulting probability distribution. (3pts) b. Find the probability that the number of people who own individual stocks is exactly six. (3pts) c. Find probability that the number of people who say they own individual stocks is at least two. (3pts) d. Find the probability that the number of people who say they own individual stocks is at most two. (3pts) e. Are the events in part c. and in part d. mutually exclusive

Answer 1

a. The mean is 3, the variance is 2.25 and the standard deviation is 1.5.

b. 0.0401 = 4.01% probability that the number of people who own individual stocks is exactly six.

c. 0.1584 = 15.84% probability that the number of people who say they own individual stocks is at least two.

d. 0.3907 = 39.07% probability that the number of people who say they own individual stocks is at most two

e. Both cases include one common outcome, that is, 2 people owning stocks, so the events are not mutually exclusive.

Explanation:

For each person, there are only two possible outcomes. Either they own stocks, or they do not. The probability of a person owning stocks is independent of any other person, which means that the binomial probability distribution is used to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
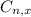`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

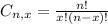
And p is the probability of X happening.

One in four people in the US owns individual stocks.

This means that
`p = (1)/(4) = 0.25`

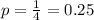
You randomly select 12 people and ask them if they own individual stocks.

This means that
`n = 12`

a. Find the mean, variance, and standard deviation of the resulting probability distribution.

The mean of the binomial distribution is:

`E(X) = np`

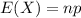
So

`E(X) = 12(0.25) = 3`

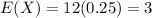
The variance is:

`V(X) = np(1-p)`

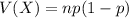
So

`V(X) = 12(0.25)(0.75) = 2.25`

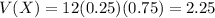
Standard deviation is the square root of the variance, so:

`√(V(X)) = √(2.25) = 1.5`

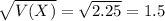
The mean is 3, the variance is 2.25 and the standard deviation is 1.5.

b. Find the probability that the number of people who own individual stocks is exactly six.

This is P(X = 6). So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 6) = C_(12,6).(0.25)^(6).(0.75)^(6) = 0.0401`

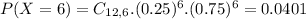
0.0401 = 4.01% probability that the number of people who own individual stocks is exactly six.

c. Find probability that the number of people who say they own individual stocks is at least two.

This is:

`P(X \geq 2) = 1 - P(X < 2)`

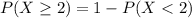
In which

`P(X < 2) = P(X = 0) + P(X = 1)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(12,0).(0.25)^(0).(0.75)^(12) = 0.0317`

`P(X = 1) = C_(12,1).(0.25)^(1).(0.75)^(11) = 0.1267`

`P(X < 2) = P(X = 0) + P(X = 1) = 0.0317 + 0.1267 = 0.1584`

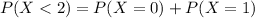
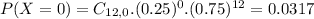
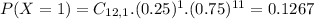
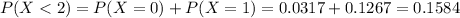
0.1584 = 15.84% probability that the number of people who say they own individual stocks is at least two.

d. Find the probability that the number of people who say they own individual stocks is at most two.

This is:

`P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(12,0).(0.25)^(0).(0.75)^(12) = 0.0317`

`P(X = 1) = C_(12,1).(0.25)^(1).(0.75)^(11) = 0.1267`

`P(X = 2) = C_(12,2).(0.25)^(2).(0.75)^(10) = 0.2323`

`P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.0317 + 0.1267 + 0.2323 = 0.3907`

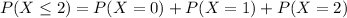
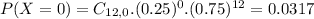
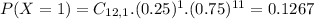
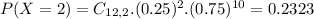
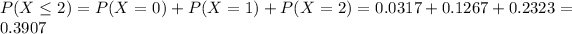
0.3907 = 39.07% probability that the number of people who say they own individual stocks is at most two.

e. Are the events in part c. and in part d. mutually exclusive

Both cases include one common outcome, that is, 2 people owning stocks, so the events are not mutually exclusive.