Given:
30-hour review course average a score of 620 on that exam.
70-hour review course average a score of 749.
To find:
The linear equation which fits this data, and use this equation to predict an average score for persons taking a 57-hour review course.
Solution:
Let x be the number of hours of review course and y be the average score on that exam.
30-hour review course average a score of 620 on that exam. So, the linear function passes through the point (30,620).
70-hour review course average a score of 749. So, the linear function passes through the point (70,749).
The linear function passes through the points (30,620) and (70,749). So, the linear equation is:
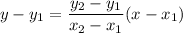
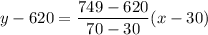
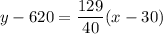
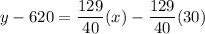
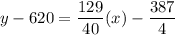
Adding 620 on both sides, we get
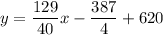
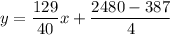
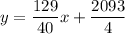
We need to find the y-value for
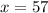 .
.

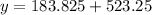
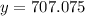
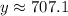
Therefore, the required linear equation for the given situation is
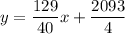 and the average score for persons taking a 57-hour review course is 707.1.
and the average score for persons taking a 57-hour review course is 707.1.