Question

The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $2000. What is the probability of randomly selecting one employee who earned less than or equal to $45,000

Answer 1

The probability of randomly selecting one employee who earned less than or equal to $45,000=0.00621

Explanation:

We are given that

Mean,
`\mu=50000`

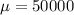
Standard deviation,
`\sigma=2000`

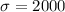
We have to find the probability of randomly selecting one employee who earned less than or equal to $45,000.

`P(x\leq 45000)=P((x-\mu)/(\sigma)\leq (45000-50000)/(2000))`

`P(x\leq 45000)=P(Z\leq-(5000)/(2000))`

`P(x\leq 45000)=P(Z\leq -2.5)`

`P(x\leq 45000)=0.00621`

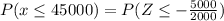
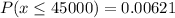
Hence, the probability of randomly selecting one employee who earned less than or equal to $45,000=0.00621