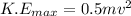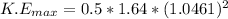Question

A 1.64 kg mass on a spring oscillates horizontal frictionless surface. The motion of the mass is described by the equation: X = 0.33cos(3.17t). In the equation, x is measured in meters and t in seconds. What is the maximum energy stored in the spring during an oscillation?

Answer 1

`K.E_(max)=0.8973J`

Step-by-step explanation:

From the question we are told that:

Mass
`m=1.64kg`

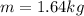
Equation of Mass

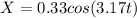`X=0.33cos(3.17t)`...1

Generally equation for distance X is

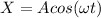`X=Acos(\omega t)`...2

Therefore comparing equation

Angular Velocity
`\omega=3.17rad/s`

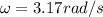
Amplitude A=0.33

Generally the equation for Max speed is mathematically given by

`V_(max)=A\omega`

`V_(max)=0.33*3.17`

`V_(max)=1.0461m/s`

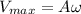
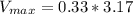
Therefore

`K.E_(max)=0.5mv^2`

`K.E_(max)=0.5*1.64*(1.0461)^2`

`K.E_(max)=0.8973J`