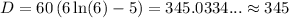Answer:
345
Explanation:
The velocity of a car over five hours is given by:
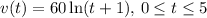
And we want to find the total distance traveled from t = 0 to t = 5.
Recall that distance is the integral of the absolute value of the velocity function. Since we want to find the total distance traveled from t = 0 to t = 5, our limits of integration are t = 0 and t = 5. Hence:
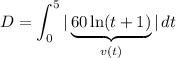
Since v(t) ≥ 0 for all t in the interval [1, 5], we can remove the absolute value. Use a calculator: