Question

A completely inelastic collision occurs between two balls of wet putty that move directly toward each other along a vertical axis. Just before the collision, one ball, of mass 3.0 kg, is moving upward at 22 m/s and the other ball, of mass 1.3 kg, is moving downward at 11 m/s. How high do the combined two balls of putty rise above the collision point

Answer 1

The height balls rise above the collision point, is approximately 7.37 meters

Step-by-step explanation:

The given parameters just before the collision are;

The mass, m₁ and velocity, v₁ of the ball moving upward are;

m₁ = 3.0 kg, v₁ = 22 m/s

The mass, m₂ and velocity, v₂ of the ball moving downward are;

m₂ = 1.3 kg, v₂ = -11 m/s (downward motion)

The type of collision = Inelastic collision

We note that the momentum is conserved for inelastic collision

Let,
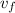`v_f`, represent the final velocity of the balls after collision, we have;

∴ Total initial momentum = Total final momentum

m₁·v₁ + m₂·v₂ = (m₁ + m₂)·
`v_f`

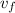
Therefore, we get;

m₁·v₁ + m₂·v₂ = 3.0 kg × 22 m/s + 1.3 kg × (-11) m/s = 51.7 kg·m/s

(m₁ + m₂)·
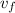`v_f` = (3.0 kg + 1.3 kg) ×

∴ 51.7 kg·m/s = 4.3 kg ×
`v_f`

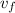
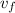`v_f` = (51.7 kg·m/s)/4.3 kg ≈ 12.023 m/s

The final velocity,
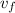`v_f` ≈ 12.023 m/s

The maximum height, h, the combined balls will rise from the point of collision, moving upward at a velocity of
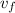`v_f` ≈ 12.023 m/s, is given from the kinetic equation of motion, v² = u² - 2·g·h, as found follows

At maximum height, we have;

`h_(max) = (v_f^2)/(2 \cdot g )`

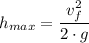
Therefore;

`h_(max) \approx (12.023^2)/(2 * 9.81 ) \approx 7.37`

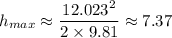
The height the combined two balls of putty rise above the collision point,
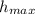`h_(max)` ≈ 7.37 m.