Answer:
The area of the square is increasing at a rate of 40 square centimeters per second.
Explanation:
The area of the square (
 ), in square centimeters, is represented by the following function:
), in square centimeters, is represented by the following function:
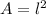 (1)
(1)
Where
 is the side length, in centimeters.
is the side length, in centimeters.
Then, we derive (1) in time to calculate the rate of change of the area of the square (
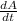 ), in square centimeters per second:
), in square centimeters per second:
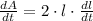
 (2)
(2)
Where
 is the rate of change of the side length, in centimeters per second.
is the rate of change of the side length, in centimeters per second.
If we know that
 and
and
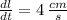 , then the rate of change of the area of the square is:
, then the rate of change of the area of the square is:

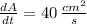
The area of the square is increasing at a rate of 40 square centimeters per second.