Answer:
The probability that exactly 12 buyers would prefer green
=0.00555
Explanation:
We are given that
p=50%=50/100=0.50
n=14
We have to find the probability that exactly 12 buyers would prefer green.
q=1-p
q=1-0.50=0.50
Using binomial distribution formula
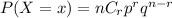
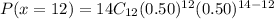
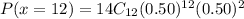
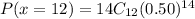
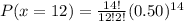
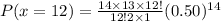
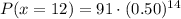
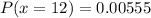
Hence, the probability that exactly 12 buyers would prefer green
=0.00555