Answer:
a) The expression for the number of bacteria is
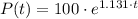 .
.
b) There are 2975 bacteria after 3 hours.
c) The rate of growth after 3 hours is about 3365.3 bacteria per hour.
d) A population of 10,000 will be reached after 4.072 hours.
Explanation:
a) The population growth of the bacteria culture is described by this ordinary differential equation:
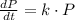 (1)
(1)
Where:
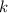 - Rate of proportionality, in
- Rate of proportionality, in
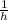 .
.
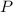 - Population of the bacteria culture, no unit.
- Population of the bacteria culture, no unit.
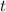 - Time, in hours.
- Time, in hours.
The solution of this differential equation is:
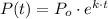 (2)
(2)
Where:
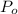 - Initial population, no unit.
- Initial population, no unit.
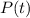 - Current population, no unit.
- Current population, no unit.
If we know that
 ,
,
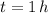 and
and
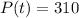 , then the rate of proportionality is:
, then the rate of proportionality is:
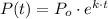
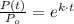
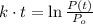
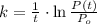
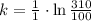
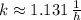
Hence, the expression for the number of bacteria is
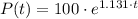 .
.
b) If we know that
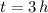 , then the number of bacteria is:
, then the number of bacteria is:
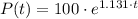
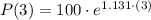
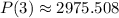
There are 2975 bacteria after 3 hours.
c) The rate of growth of the population is represented by (1):
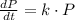
If we know that
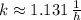 and
and
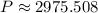 , then the rate of growth after 3 hours:
, then the rate of growth after 3 hours:
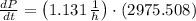
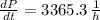
The rate of growth after 3 hours is about 3365.3 bacteria per hour.
d) If we know that
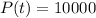 , then the time associated with the size of the bacteria culture is:
, then the time associated with the size of the bacteria culture is:
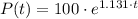
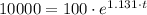
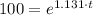
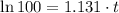
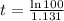
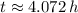
A population of 10,000 will be reached after 4.072 hours.