Question

A bacteria culture initially contains 100 cells and grows at a rate proportional to its size. After an hour the population has increased to 310.

(a) Find an expression for the number of bacteria after
hours.
(b) Find the number of bacteria after 3 hours.
(c) Find the rate of growth after 3 hours.
(d) When will the population reach 10,000?

Answer 1

a) The expression for the number of bacteria is
`P(t) = 100\cdot e^(1.131\cdot t)`.

b) There are 2975 bacteria after 3 hours.

c) The rate of growth after 3 hours is about 3365.3 bacteria per hour.

d) A population of 10,000 will be reached after 4.072 hours.

Explanation:

a) The population growth of the bacteria culture is described by this ordinary differential equation:

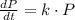`(dP)/(dt) = k\cdot P` (1)

Where:

`k` - Rate of proportionality, in
`(1)/(h)`.

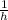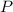`P` - Population of the bacteria culture, no unit.

`t` - Time, in hours.

The solution of this differential equation is:

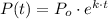`P(t) = P_(o)\cdot e^(k\cdot t)` (2)

Where:

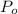`P_(o)` - Initial population, no unit.

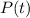`P(t)` - Current population, no unit.

If we know that
`P_(o) = 100`,
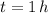`t = 1\,h` and
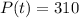`P(t) = 310`, then the rate of proportionality is:

`P(t) = P_(o)\cdot e^(k\cdot t)`

`(P(t))/(P_(o)) = e^(k\cdot t)`

`k\cdot t = \ln (P(t))/(P_(o))`

`k = (1)/(t)\cdot \ln (P(t))/(P_(o))`

`k = (1)/(1)\cdot \ln (310)/(100)`

`k\approx 1.131\,(1)/(h)`

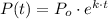
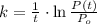
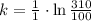
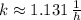
Hence, the expression for the number of bacteria is
`P(t) = 100\cdot e^(1.131\cdot t)`.

b) If we know that
`t = 3\,h`, then the number of bacteria is:

`P(t) = 100\cdot e^(1.131\cdot t)`

`P(3) = 100\cdot e^(1.131\cdot (3))`

`P(3) \approx 2975.508`

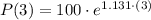
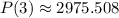
There are 2975 bacteria after 3 hours.

c) The rate of growth of the population is represented by (1):

`(dP)/(dt) = k\cdot P`

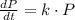
If we know that
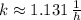`k\approx 1.131\,(1)/(h)` and
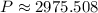`P \approx 2975.508`, then the rate of growth after 3 hours:

`(dP)/(dt) = \left(1.131\,(1)/(h) \right)\cdot (2975.508)`

`(dP)/(dt) = 3365.3\,(1)/(h)`

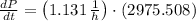
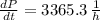
The rate of growth after 3 hours is about 3365.3 bacteria per hour.

d) If we know that
`P(t) = 10000`, then the time associated with the size of the bacteria culture is:

`P(t) = 100\cdot e^(1.131\cdot t)`

`10000 = 100\cdot e^(1.131\cdot t)`

`100 = e^(1.131\cdot t)`

`\ln 100 = 1.131\cdot t`

`t = (\ln 100)/(1.131)`

`t \approx 4.072\,h`

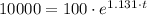
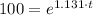
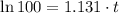
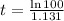
A population of 10,000 will be reached after 4.072 hours.