Answer:

Explanation:
Given information:
Contents of Jar 1:
- 20 green marbles
- 4 white marbles
- total marbles = 20 + 4 = 24
Contents of Jar 2:
- 60 black marbles
- 20 white marbles
- total marbles = 60 + 20 = 80
Probability Formula
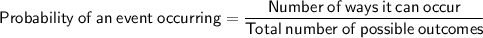
Therefore:


As the events are independent (i.e. drawing a marble from one jar does not influence or affect drawing a marble from the other jar), we can use the independent probability formula:
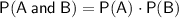
Therefore, the probability that a white marble will be drawn from both jars is:
