Answer:
The equation of
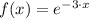 by Maclaurin series is
by Maclaurin series is
 .
.
Explanation:
The Maclaurin series for
 is defined by the following formula:
is defined by the following formula:
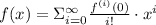 (1)
(1)
Where
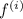 is the i-th derivative of the function.
is the i-th derivative of the function.
If
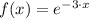 , then the formula of the i-th derivative of the function is:
, then the formula of the i-th derivative of the function is:
 (2)
(2)
Then,
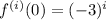 (2b)
(2b)
Lastly, the equation of the trascendental function by Maclaurin series is:
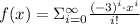
 (3)
(3)