Answer:
The motion of the particle describes an ellipse.
Explanation:
The characteristics of the motion of the particle is derived by eliminating
 in the parametric expressions. Since both expressions are based on trigonometric functions, we proceed to use the following trigonometric identity:
in the parametric expressions. Since both expressions are based on trigonometric functions, we proceed to use the following trigonometric identity:
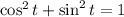 (1)
(1)
Where:
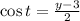 (2)
(2)
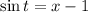 (3)
(3)
By (2) and (3) in (1):
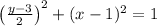
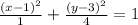 (4)
(4)
The motion of the particle describes an ellipse.